Game of Life in JavaScript - Part 1
I fancy making something now so this is a small series about implementing Conway’s Game of Life, using JavaScript with TDD.
Normally, I pretty much know exactly what I will do in my blog posts, but not this time. Oops! So, instead, follow along with me whilst I slowly (maybe) build the Game of Life in my browser.
Here’s the high-level plan, preceded by tests (that might alter at ground-level!).
| Part | Objectives |
|---|---|
| 1 | Describe the rules and show some pretty pictures |
| 2 | Set up Jest and have a basic test running |
| 3 | Define my playing area for the game and initialise it |
| 4 | Turn that logical representation into something I can see |
| 5 | Implement rule 1 |
| 6 | Implement rule 2 |
| 7 | Implement rule 3 |
| 8 | Wrap up |
I may condense some of those parts, you just never know, but if I do, I will edit this and pretend I nailed my planning!
Let’s begin with a bit of mathematical history.
Conway
It all started in 1968 with a mathematician named John Horton Conway. He’d been experimenting with the idea of doing something with cellular automatons to come up with something “interesting and unpredictable”. But what is a cellular automaton? In basic terms (the only ones I have on my budget), its the idea that you have a grid of cells where each cell can have a fixed number of states. In this case, that’s either “on” or “off”, a bit like a computer monitor’s display or some bits in RAM. What happens next is governed by rules and specifically, rules about which cells are “on” or “off” based on neighbouring cells.
To be successful though, it needed to satisfy John Von Neumann’s two principles which were that:
- it should be able to reproduce, and
- simulate a Turing Machine.
I know, this is starting to look like a big rabbit-hole moving from one definition to another! What you need to know is that von Neumann was considered the foremost mathematician of his time (1903-1957) and a Turing machine is a hypothetical machine which can implement any algorithm simply by moving forwards and backwards on a computer tape (remember, this was the 1940s!).
That’s the background, but what about the rules?
The Rules
These can be condensed into 3 main things that need to be implemented:
- Any live cell with two or 3 live neighbours survives.
- Any dead cell with 3 live neighbours becomes a live cell.
- All other live cells die in the next generation. Similarly, all other dead cells stay dead.
In practice, this means that you zip through the grid looking at each cell and working out what cells are around it. Depending on that, and of course, these rules, governs whether a cell sprouts into life (becomes “on”), stays alive (remains “on”) or dies (goes to the great “off” in the sky).
Let’s try and make this a bit more concrete with some examples.
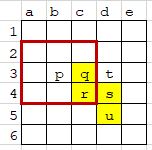
Here we have a 2 dimensional grid, labelled with columns (a-e) and rows (1-5). Some of the cells have been highlight - the yellow ones are “on” or alive, and the clear cells, “off” or dead.
I’ve also placed some letters in the cells and it’s the one with a “p” in it that I want you to focus on.
“p” has not had a good start to life and is currently dead (“off”). Around it, you can see a red box - the squares that lie just inside that box are what are known as “p”‘s neighbouring cells. All is not lost, so let’s see if any of our 3 rules can bring it back from the dead.
Rule 1 is all about any live cell. “p” is dead, so we move on.
Rule 2 says that any dead cell (yep, “p” is dead) with 3 live neighbours can spring into life. We can see that cell 3c and 4c are live, but all the others are dead, so drat, he remains dead too.
Rule 3 states (ignoring the live bit) that all dead cells stay dead.
So that’s it, “p”, you remain dead.
How about “s” in 4d? Things are looking up.
Rule 1 dictates that any live cell (and “s” is live) with 2 or 3 neighbours, will remain alive. In this case, “s” has 3 live neighbours: 3c, 4c and 5d, so it hangs in there!
Rules 2 and 3 don’t apply in this case.
One more example for the road. Take a look at “t” in 3d.
Rule 1 is another live cell rule, so we can ignore it.
Rule 2 is more interesting because it involves dead cells. It tells us that if a dead cell has 3 live neighbours, it can spring into life itself. In this case, 3c, 4c and 4d are all live and add up to 3 cells, so we have a winner!
Rule 3 does not apply.
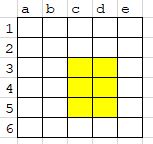
After one whole iteration, this is what the grid would look like.
Phew - you made it this far so it couldn’t have been that dry, could it? Let’s end with a few moving pictures, courtesy of Wikipedia.
Some Notable Shapes
A Blinker

A Beacon
A Glider

Next Time
Next time, we’ll look at installing Jest and getting a basic test or two running, ready to start implementing our own version of Game of Life.
Hi! Did you find this useful or interesting? I have an email list coming soon, but in the meantime, if you ready anything you fancy chatting about, I would love to hear from you. You can contact me here or at stephen ‘at’ logicalmoon.com